Contents

Chapter 1
Introduction

1.1 Kranc

Kranc is a suite of Mathematica-based computer-algebra packages, which comprise a toolbox to convert certain (tensorial) systems of partial differential evolution equations to parallelized C code for solving initial boundary value problems. Kranc can be used as a rapid prototyping system for physicists or mathematicians handling complicated systems of partial differential equations, but through integration into the Cactus computational toolkit it is also possible to produce efficient parallelized production codes. Our work is motivated by the field of numerical relativity, where Kranc is used as a research tool by the authors. The initial version of Kranc was described in [?], and subsequent enhancements in [?]. The user-visible portion of Kranc has subsequently been redesigned. The material in this document is drawn from these two sources, and has been updated to be consistent with the current version of Kranc.

1.2 Cactus

The Cactus Computational Toolkit is an open-source problem solving environment originally developed in the numerical relativity community. It is arranged as a central flesh and a collection of modules called thorns which all communicate with the flesh. Many thorns are provided, and the user writes additional thorns in C or Fortran which solve their particular physics problem. Cactus is particularly suited to the numerical solution of time dependent partial differential equations.

Kranc is concerned with taking an abstract mathematical description of a system of PDEs and producing working computer code. It does this by generating Cactus thorns, allowing use of all the infrastructure provided by Cactus.

For example, Kranc makes uses of existing Cactus thorns which provide:

• Parameter file parsing.
• Memory management for variables associated with the computational grid.
• Scheduling of parts of the code based upon parameters.
• Standard efficient time integrators such as fourth order Runge-Kutta via the MoL thorn written by I. Hawke.
• Mesh refinement [?]; i.e., using variable resolution across the numerical grid, so that the computational resources are focused on interesting parts of the simulation.
• Automatic parallelization of the code via MPI to run across multiple processors on a supercomputer or cluster, both to improve computational speed and to use larger grids than can be stored in the memory of a single node.
• Output of grid variables to permanent storage in a structured format, for example HDF5.

These tasks are completely separate from the physics and numerical analysis side of the problem, but are necessary in most numerical codes.

1.3 Overview of the Kranc system

Kranc provides a Mathematica function called CreateThorn. The user must construct arguments and data structures for this function describing the thorn they wish to create. Kranc generates code and Cactus CCL files for:

• Declaring the grid functions which the simulation will use;
• Registering the grid functions for the evolved variables with the MoL thorn;
• Computing the right hand sides of evolution equations so that the time integrator can compute the evolved variables at the next time step;
• Computing finite differences, both using built-in definitions of standard centred finite differencing operators, as well as allowing the user to create customised operators;
• Performing a user-specified calculation at each point of the grid.

User-specified calculations will typically set certain grid variables as functions of others, and can be used for various purposes including making a change of variables or computing intermediate or analysis quantities from evolved variables.

The most important data structure in Kranc is a Calculation structure. It encapsulates the idea of assigning new values to grid functions in a loop over grid points based upon evaluating expressions involving other grid functions. Calculations contain lists of assignment statements for different grid functions, and these are evaluated at each point on the grid. Calculations can also contain temporary variables called shorthands into which are placed intermediate expressions which are used later in the calculation. Calculations also contain additional information needed by the Kranc system, such as a name for the calculation.

Chapter 2
Using Kranc

2.1 Data structures

The user needs to pass information to Kranc in a structured way. Mathematica does not have the concept of a C++ class or a C structure, in which collections of named objects are grouped together for ease of manipulation. Instead, we have defined a Kranc structure as a list of rules of the form key -> value. We have chosen to use the Mathematica rule symbol “->” for syntactic convenience.

For example, one might describe a person using a “Person” structure as follows:

Based on this concept a number of data structures have been defined which will be used to describe the thorn to construct. Each of these data structures is introduced below.

2.1.1 Data structure: Calculation

Calculation structures are the core of the Kranc system. A Calculation structure has the following form:

Only the Name key is required; all the others take default values if omitted.

Name

The name of a calculation is a string which will be used as the function name in Cactus, as well as the base of the filename of the source file implementing the calculation in the generated thorn.

Example:

Equations

The equation list is a list of assignments to perform in the calculation loop. Each equation is of the form

When the calculation is performed, for each point in the grid, expression is evaluated and placed into the grid function variable. Here expression may contain partial derivatives of grid functions which have been defined in a PartialDerivatives structure. variable may be either a grid function or a shorthand. Using the notation dot[gf] for variable represents a time derivative of the grid function gf; this should be used when the calculation is scheduled in MoL_CalcRHS for calculating the right hand sides of the evolution equations.

It is possible to use the same variable (either a grid function or a shorthand) on both the left hand side and the right hand side of an equation assignment. However, in that case the variable must not be differentiated on the right hand side, as this would lead to a result which depended on the ordering of the loop over the grid points, which is almost certainly not what is intended. Kranc will detect such a differentiation and abort with an error. See the option ProhibitAssignmentToGridFunctionsRead to CreateThorn in Sec.?? if you want to prohibit such assignments altogether.

Schedule

This is a list of Cactus schedule specifications describing when in the simulation the calculation will be performed. Multiple schedule strings can be provided to allow the calculation to be scheduled at multiple points. Omitting the schedule information causes Kranc to schedule the calculation automatically. Currently, this is used for analysis quantities which are scheduled in MoL_PseudoEvolution and have boundary conditions applied after them.

Examples:

Shorthands

This is a list of variables which are to be considered as shorthands for the purposes of this calculation. These are temporary variables which are defined locally in the loop and are not grid functions defined over the whole grid. They are used as intermediate variables when setting more complicated grid functions. Since they are defined only pointwise, they cannot be differentiated.

Examples:

Where

Different calculations need to be evaluated on different portions of the numerical grid. For example, a calculation which implements a boundary condition needs to be performed on the boundary points only. A calculation which contains derivatives needs to be performed on the interior of the grid only. A calculation which does not contain derivatives can be performed even in the ghost zones, so that a potentially time-consuming synchronisation can be avoided. The Where option can have values of Everywhere, Interior or Boundary corresponding to these choices. There is currently no check that a calculation containing derivatives is not performed on the entire grid, nor that the number of ghost zones selected by the user at run time is compatible with the finite differencing operator chosen.

Examples:

Conditional

This key allows a calculation to be performed conditionally based on parameters set by the user at run time. Setting

where <expr> is a boolean expression over parameter names and literal values will cause the calculation to be performed only if the expression evaluates to true at runtime.

The expression can contain && (and), || (or), ! (not) operators as well as symbolic parameter names and numeric and string constants.

Comparison of parameters with literal values can be expressed using <param> == <value> or <param> != <value>.

In the case that a parameter name cannot be represented as a Mathematica symbol (e.g. if it contains underscores), it should be represented as Parameter[<string>] where <string> is a string containing the parameter name.

Note that the construct <string> == <string> will be evaluated immediately by Mathematica as either True or False, and so should not be used.

Example:

ConditionalOnKeyword

(deprecated: use Conditional instead)

This key allows a calculation to be performed conditionally based on the value of a parameter set by the user at run time. Setting

where <param> is a string naming a keyword parameter defined in the KeywordParameters option to CreateThorn will cause the calculation to be performed only if that parameter is set to <value>.

Example:

ConditionalOnKeywords

(deprecated: use Conditional instead)

The ConditionalOnKeywords key takes a list of {<param>, <value>} pairs as described under ConditionalOnKeyword. All the parameters must match for the calculation to be scheduled.

ConditionalOnTextuals

(deprecated: use Conditional instead)

This key can be set to a string which is used verbatim in the Cactus schedule.ccl file. Any valid Cactus conditional string can be used.

CollectList

The arrangement of the terms in the equations can have a significant effect on both compile time and run time. It is often helpful to tell Mathematica to collect the coefficients of certain types of term, rather than expanding out entire expressions. The user can include a CollectList entry in a calculation; this is a list of variables whose coefficients should be collected during simplification.

NoSimplify

Setting this option to True stops Kranc from simplifying the right hand sides of expressions in this calculation. This could be used because the user has found a way of writing the expressions which leads to faster code than if Kranc’s simplification is used, or because the expressions are so complicated that the simplification takes a very long time to perform.

Example:

DeclarationIncludes

This is a list of filenames which will be #includeed in the generated code inside the calculation function but before the loop over grid points.

Calculation Example

The following example is taken from the Kranc implementation of the NOR formulation of Einstein’s equations. It is a calculation which describes the time evolution equation for the lapse function α in harmonic slicing. It uses the TensorTools package to represent tensorial quantities.

(The MatrixInverse function is provided by TensorTools to generate an expression for the inverse matrix.)

2.1.2 Data structure: PartialDerivatives

The user can define partial derivative operators and associated finite difference approximations of these operators. This allows different discretizations of the PDE system.

A finite difference operator maps grid functions to grid functions. We restrict to those operators which are polynomials in shift operators. In one dimension, the shift operator E₊ is defined as

The PartialDerivatives structure is a list of definitions of partial derivative operators in terms of finite difference approximations:

where name is the name for the partial derivative, and defn is an algebraic expression in shift operators representing the difference operator. The shift operator E_+i is written as shift[i]. The form spacing[i] can be used in defn to represent the grid spacing in the i direction. The parameters i, j, … are used in defn to represent the direction of differentiation for the first, second, etc. derivatives. Partial derivatives with the same name but a different number of arguments (i.e., for first and second derivatives) are allowed in the PartialDerivatives structure.

Since the definitions of the difference operators are written in terms of Mathematica expressions, higher level operators can be constructed from shift and spacing. For example, Kranc predefines

As an example, we give here a PartialDerivatives structure containing the definition of the standard second order accurate difference operators, as well as the D₀² discretization.

In a calculation, a partial derivative is written in the form

For example, a one dimensional advection equation ∂_tu = ∂_xu with semidiscrete form ∂_tv_j = D₀₁v_j could be described as

The PartialDerivatives structure can also be used to define operators for artificial dissipation. Given a semidiscrete scheme

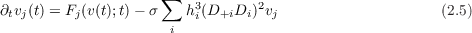
We define a differencing operator Diss2nd in the PartialDerivatives structure with no directional arguments

using the standard Mathematica function for summations. An evolution equation representing the advection equation with dissipation could then be written as

A PartialDerivatives structure is given as an argument to the thorn generation function CreateThorn.

2.1.3 Data structure: GroupDefinition

A GroupDefinition structure lists the grid functions that are members of a specific Cactus group. A list of such structures should be supplied to CreateThorn function so that Kranc can determine which group each grid function belongs to.

The form of a GroupDefinition structure is

groupname is a string, and the variables are symbols. For example,

would represent a group called sol with variables phi and pi.

The group name can be prefixed with the name of the Cactus implementation that provides the group followed by two colons (e.g. “ADMBase::metric”).

2.2 TensorTools

The TensorTools package was written specifically for the Kranc system, though it is in no way tied to it. It is necessary to perform certain operations on tensorial quantities, and there was no free software available which met the requirements.

2.2.1 Representation of tensor quantities

Tensorial expressions are entered in the same syntax as is used by MathTensor, a commercial tensor manipulation package which can be used instead of TensorTools. An abstract tensor consists of a kernel and an arbitrary number of abstract indices, each of which can be upper or lower. Abstract indices are alphabetical characters (a-z, A-Z) prefixed with either an l or a u depending on whether the index is considered to be lower or upper. The tensor is written using square brackets as

For example, T_a ^b would be written as T[la,ub]. There is no automatic index raising or lowering with any metric. Entering a tensorial expression causes it to be displayed in standard mathematical notation:

Internally, tensors are represented as Tensor[kernel, TensorIndex[label, type], ...] where label is the alphabetical index, and type is either “u” or “l” depending on the position of the index. This representation helps in pattern matching, and allows TensorTools to identify whether a certain object is a tensor or not.

2.2.2 Expansion of tensorial expressions into components

As an example, the TensorTools function MakeExplicit converts an expression containing abstract tensors into a list of component expressions:

Note here that there is no distinction made between upper and lower indices in the component form. TensorTools was written mainly for automated code generation rather than symbolic manipulation; different kernels should be used for the different forms if this is a problem.

2.3 Creating a Kranc thorn

Prototype: CreateThorn[groups, directory, thornName, namedArgs]

Note that if you want to use TensorTools tensors in calculations, you must call the CreateThornTT function instead of this one. It takes the same arguments, but they can be tensorial in nature.

Positional Arguments

Named Arguments

Chapter 3
Additional Features

In addition to the basic functionality described in Chapter 2, Kranc provides a number of additional features. Each of these features can be used independently, and are typically enabled by an option of the form Use* -> True in the call to CreateThorn.

3.1 Jacobians

Kranc allows the user to apply an arbitrary user-defined Jacobian transformation (provided in a grid function) to all derivatives. This feature is enabled by setting UseJacobian -> True in the options to CreateThorn or CreateThornTT. This can be used to generate codes which work with multi-block schemes. The use of the Jacobian is determined at run time, so a single code can be generated which will work both with and without a Jacobian being present.

Kranc does not provide the Jacobian grid function; it might be provided by an external infrastructure (for example for multi-block schemes), or could be provided easily in the user’s thorn, or another Kranc-generated thorn. Wherever the Jacobian is provided, it must adhere to the following conventions. There should be one Cactus group for the components of the Jacobian matrix and another for the components of its first spatial derivative (this is necessary for systems containing second spatial derivatives). The components should be real-valued grid functions declared in a similar manner to the following:

The names of the groups and variables are not important, but the order of the variables within the groups is critical.

The GenericFD thorn provides two parameters, jacobian_group and jacobian_derivative_group which should be set by the user in their parameter file to the names of the Jacobian and Jacobian derivative groups. With the above Jacobian definition, provided by a thorn with implementation MyCoordTransform the user would set

The partial derivatives, associated with certain finite difference operators, specified in the user’s calculation, will then be multiplied by the Jacobian. If the user specifies the following,

the code that will actually be generated will be

Note:

• The Jacobian multiplication introduces an additional performance cost to the simulation, so it should not be enabled unless necessary.
• If the Jacobian parameters are left unset, the partial derivatives will not be multiplied by any Jacobian, and the performance will be only slightly worse than if UseJacobian was not set and the Jacobian code was not generated (the extra cost comes from the use of run-time conditionals).
• The parameter GenericFD::jacobian_identity_map can be used with multi-block systems to prevent the use of the Jacobian on one of the maps. Set this parameter to the map number (e.g. 0) where the Jacobian should not be applied. This can lead to a significant performance improvement.

Appendix A
Kranc internal design

Kranc is composed of several Mathematica packages. Each of these human readable scripts performs a distinct function. The diagram in Figure A illustrates the relationships between the Kranc packages KrancThorns, TensorTools, CodeGen, Thorn and MapLookup, which are described in the following subsections.

Separating the different logically independent components of Kranc into different packages promotes code reuse. For example, none of the thorn generation packages need to know anything about tensors, and none of the packages other than CodeGen need to know the programming language in which the thorn is being generated (C or Fortran). We have chosen to define several types of thorn (setter, evaluator, etc.) but the mechanics of producing a thorn implemented in Thorn and CodeGen are completely independent of this decision.

A.0.1 Package: CodeGen

During the development of the Kranc system, we explored two different approaches to generating Cactus files using Mathematica as a programming language. Initially, a very straightforward system was used whereby C statements were included almost verbatim in the Mathematica script and output directly to the thorn source file. This approach has two main deficiencies:

• The same block of text might be used in several places in the code. When a bug is fixed in one place, it must be fixed in all.
• It is not easy to alter the language that is produced. For example, it is difficult to output both C and Fortran.
• The syntax in the Mathematica source file is ugly, with lots of string concatenation, making it difficult to read and edit.

The CodeGen package provides functions to solve these problems. To address the first problem, Mathematica functions are used to represent each block of code. This allows the block to be customized by giving the function arguments. By making this abstraction, it became very easy to change between outputting C and Fortran.

Fundamental to the system is the notion of a block; in Mathematica terms this can be either a string or a list of blocks (this definition is recursive). All the CodeGen functions return blocks, and the lists are all flattened and the strings concatenated when the final source file is generated. This is because it is syntactically easier in the Mathematica source file to write a sequence of statements as a list than to concatenate strings.

Many programming constructs are naturally block-structured; for example, C for loops need braces after the block of code to loop over. For this reason, it was decided that CodeGen functions could take as arguments any blocks of code which needed to be inserted on the inside of such a structure.

A.0.2 Package: Thorn

The Thorn package is used by all the different thorn generators to construct the final Cactus thorn. It takes care of the mechanics of writing files to storage and parsing the Kranc structures necessary for writing parameter configuration files, grid function definitions etc.